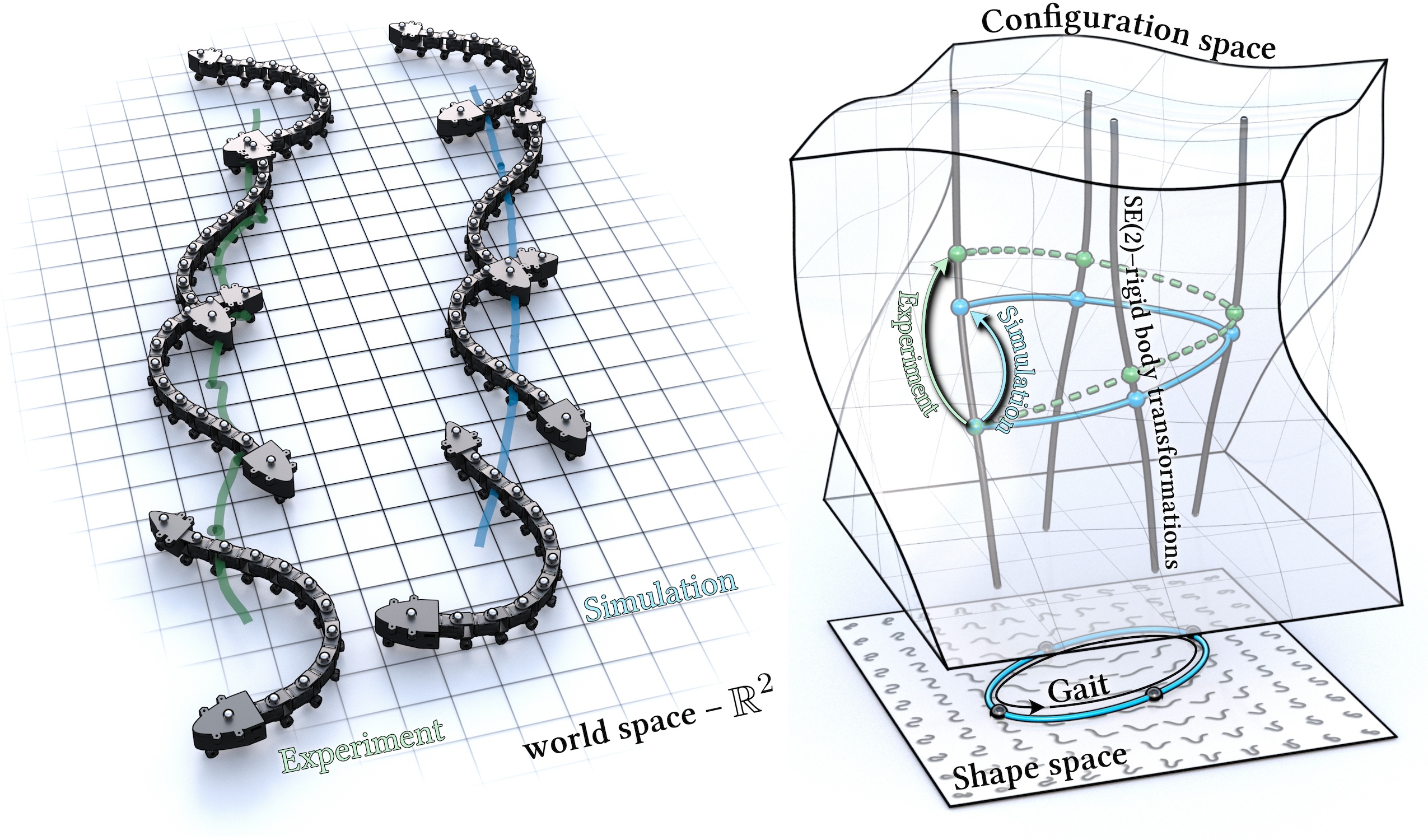
Limbless organisms of all sizes use undulating patterns of self-deformation to locomote. Geometric mechanics, which maps deformations to motions, provides a powerful framework to formalize and investigate the theoretical properties and limitations of such modes of locomotion. However, the inherent level of abstraction poses a challenge when bridging the gap between theory or simulations and laboratory experiments.
We investigate the challenges of modeling motion trajectories of an undulating robotic locomotor by comparing experiments and simulations performed with a variational integrator. Despite the extensive simplifications that the model based on a geometric variation principle entails, the simulations show good agreement on average. Notably, our approach merely requires the knowledge of the dissipation metric---a Riemannian metric on the configuration space, which can in practice be approximated by means closely resembling resistive force theory.
|